Codeforce Raising_Bacteria Task

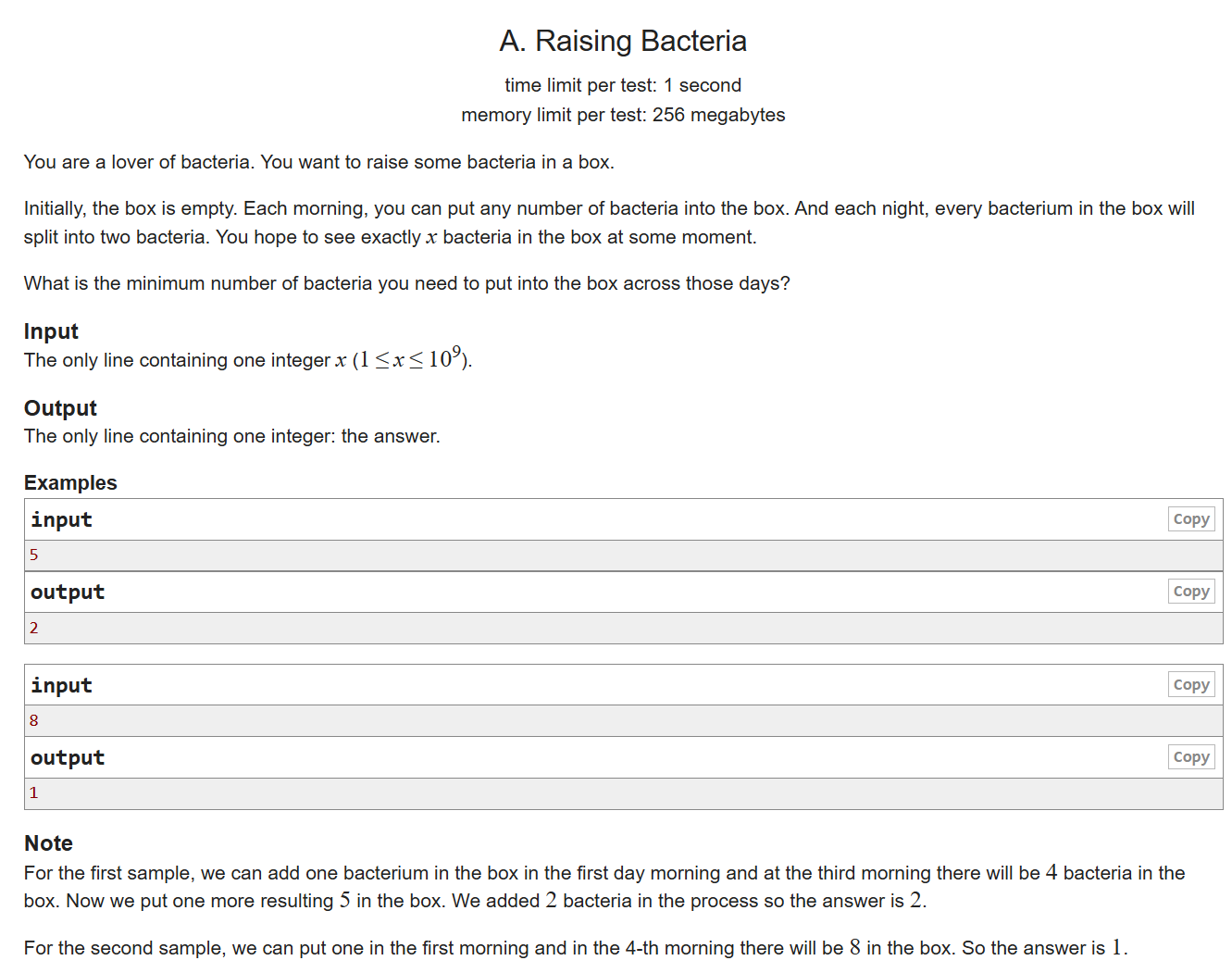
题目描述

思路

这道题主要考察的是对二进制的理解。

假设我们在第 $i$ 天会放入数量为 $x_i$ 的细菌，那么 $n$ 天之后会得到 $\sum^n_{i=0}x_i \cdot 2^i$ 。

所以给定一个数 $x$ ，我们需要找到一组 $[x_0,x_1,…,x_n]$ ，使得 $\sum^n_{i=0}x_i$ 最小，并且 $\sum^n_{i=0}x_i \cdot 2^i = x$ ，即

假设 $\sum^n_{i=0}a_i \cdot 2^i$ 为 $x$ 的二进制展开。我们现在证明 $[a_0,…,a_n]$ 正是这个最优化问题的解：

首先很显然 $[a_0,…,a_n]$ 满足上面的条件（s.t. 的部分）。假设现在存在 $[b_0,…,b_n]$ 使得 $\sum^n_{i=0}b_i \cdot 2^i = x$ 并且 $\sum^n_{i=0}b_i \leq \sum^n_{i=0}a_i$，因为二进制展开永远是唯一的，不难得到 $\forall i : a_i = b_i$。

所以我们这道题需要做的就是计算 $\sum^n_{i=0}a_i$，也就是说只需要数 $x$ 的二进制表达里一共有多少个1。

代码

C++

1
2
3
4
5
6
7
8
9
10
11

#include <iostream>
#include <bitset>
using namespace std;

int main() {
    int x;
    cin >> x;
    cout << __builtin_popcount(x) << endl;
    // __builtin_popcount(x) 会返回整数 x 的二进制中 1 的个数。
    return 0;
}

也可以原始一点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include <iostream>
using namespace std;

int main() {
    int x;
    cin >> x;
    int count = 0;
    while (x > 0) {
        if (x % 2 == 1) {
            count++;
        }
        x /= 2;
    }
    cout << count << endl;
    return 0;
}