量子计算入门

Introduction

基本概念

量子比特（Quantum bits, qubits）

普通的比特（bit）只能取两种离散值：0和1。

而量子比特（Quantum bits, qubits）则是处于0和1的叠加态（superposition）：一个量子比特的一般态（quantum state）$|\psi\rangle$ 一般写作：

$$|\psi\rangle = \alpha\,|0\rangle + \beta\,|1\rangle, \ \ \alpha,\beta \in \mathbb{C}$$

满足

$$|\alpha|^2 + |\beta|^2 = 1$$

这里的符号 $|\psi\rangle$ 叫做 Ket-notation。

我们可以将$|0\rangle,|1\rangle$ 当成一个basis，然后将qubit的所有状态看成是一个二维空间的子集，所以我们也可以写成

$$|\psi\rangle = \begin{pmatrix} \alpha \\ \beta \end{pmatrix}$$

当然，在量子比特被观测时，我们只会得到0或者1的结果。其中观测到0的概率为 $|\alpha|^2$，观测到1的概率为 $|\beta|^2$。观测行为本身也会改变qubit。如果观测到0，那么qubit会变成 $|\psi\rangle = |0\rangle$，如果观测到1，那么qubit会变成 $|\psi\rangle = |1\rangle$。

需要注意的是我们无法直接观测到一个量子比特的状态，即无法直接测量$\alpha$和$\beta$的值。

当然我们还可以用其他方法来表示量子比特：

因为$|\alpha|^2 + |\beta|^2 = 1$，所以当$\alpha$和$\beta$是实数时，一定存在一个$\theta\in \mathbb{R}$ 使得：

$$\alpha = cos(\frac{\theta}{2}) , \ \ \beta = sin(\frac{\theta}{2})$$

推广到复数便可以得到：（因为每个复数都可以写成极坐标的形式： $c = re^{i\gamma} = |c| \cdot e^{i\gamma}$）

$$\alpha = e^{i\gamma} cos(\frac{\theta}{2}) , \ \ \beta = e^{i(\gamma + \varphi)}sin(\frac{\theta}{2})$$

因此我们可以将$|\psi\rangle$写成：

$$\begin{align} |\psi\rangle &= e^{i\gamma} cos(\frac{\theta}{2}) \ |0\rangle + e^{i(\gamma + \varphi)}sin(\frac{\theta}{2}) \\ &= e^{i\gamma}\Bigl(cos(\frac{\theta}{2}) \ |0\rangle + e^{i\varphi}sin(\frac{\theta}{2})\Bigl) \end{align}$$

其中$ \theta \in [0, \pi],\quad \varphi, \gamma \in [0, 2\pi)$。

由于$e^{i\gamma}$对我们来说并不重要（后面会详细讲），所以一个qubit实际上只需要2个实数参数（$\theta, \varphi$）。由此每个qubit都对应 Bloch Sphere 的surface上的一个点：

$$r = \begin{pmatrix} cos(\varphi)sin(\theta)\\ sin(\varphi)sin(\theta)\\ cos(\theta) \end{pmatrix}$$

Bloch Sphere：

注意，$|0\rangle$和$|1\rangle$对应的$\theta$的值分别为0和$\pi$，所以他们对应Bloch Sphere的2个极点（poles）。

单量子比特门（Single qubit gate）

我们一般用一个complex unitary matrix U来表示qubit的状态变化：

$$|\psi\rangle' = U \cdot |\psi\rangle$$

对应的电路图一般这样画：

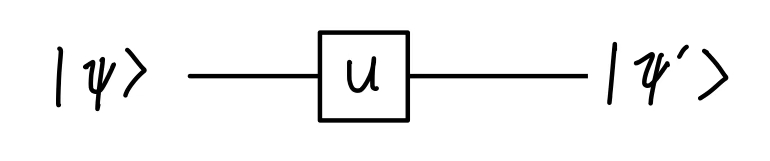
下面来看一些例子：

以下3个（X,Y,Z）叫做Pauli matrices:

Pauli-X gate:

$$X = \sigma_1 = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$$

注意到：

$$X|0\rangle = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix}= |1\rangle$$ $$X|1\rangle = |0\rangle$$

Pauli-Y gate:

$$Y = \sigma_2 = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}$$

Pauli-Z gate:

$$Z = \sigma_3 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$$

注意到Z不会改变$|0\rangle$，但是会改变$|1\rangle$的系数的符号：

假设

$$\begin{align} Z \ |\psi\rangle &= cos(\frac{\theta}{2}) \ |0\rangle - e^{i\varphi}sin(\frac{\theta}{2})\\ &= cos(\frac{\theta}{2}) \ |0\rangle + e^{i\pi}e^{i\varphi}sin(\frac{\theta}{2})\\ &= cos(\frac{\theta}{2}) \ |0\rangle + e^{i(\varphi+\pi)}sin(\frac{\theta}{2}) \end{align}$$

这同样意味着$|\psi\rangle $会沿着Z轴旋转$180^\circ$。

而 Pauli vector 指的则是 $\sigma = (\sigma_1,\sigma_2,\sigma_3) = (X,Y,Z)$。（a vector of $2\times 2$ matrices）