大纲/总结
2.Grundbegriffe
2.1 Grammatiken
2.2 Die Chomsky-Hierarchie:
Typ 0 (Phrasenstruktur), 1 (Kontextsensitive), 2 (Kontextfreie), 3 (Rechtslinear, Regulär)
3.Reguläre Sprachen (Typ 3)
3.1 Deterministische endliche Automaten
3.2 Von rechtslinearen Grammatiken zu DFA (und zurück)
3.3 NFAs mit epsilon-Übergängen
3.4 Reguläre Ausdrücke
3.5 Von NFA zu RE als Lösung eines Gleichungssystems:
推导NFA对应的RE,以及从RE对应的NFA。
3.6 Rechnen mit regulären Ausdrücken:
一些等价的RE。
3.7 Abschlusseigenschaften regulärer Sprachen:
regulärer Sprachen的交并集,补集,乘集等都是regulärer的。
3.8 Pumping Lemma:
Reguläre Sprache的特殊性质,可以用于证明某个Sprache不是regulär的。
3.9 Entscheidungsverfahren:
以下几个问题的可解性以及复杂度:Wortproblem, Leerheitsproblem, Endlichkeitsproblem, Äquivalenzproblem。
3.10 Minimierung endlicher Automaten:
每个DFA都能(利用等价类)化简到minimal。
4.Kontextfreie Sprachen (Typ 2)
4.1 Kontextfreie Grammatiken
Syntaxbaum,复习定义,新缩写:CFG (Kontextfreie Grammatik),CFL (Kontextfreie Sprache)。
4.2 Induktive Definitionen, Syntaxbäume und Ableitungen
Wort的推导/生成都有一个对应的Syntaxbaum。
4.3 Die Chomsky-Normalform
epsilon-Produktion,Kettenproduktion,(如何构造)Chomsky-Normalform,Greibach-Normalform。
4.4 Das Pumping-Lemma für kontextfreie Sprachen:
和之前的类似,适合用于证明某个Sprache不是kontextfrei的。
4.5 Abschlusseigenschaften:
Vereinigung,Konkatenation,Stern,Spiegelung后的都还是kontextfrei,但是交集,补集不一定是了。
4.6 Algorithmen für kontextfreie Grammatiken
4.7 Der Cocke-Younger-Kasami-Algorithmus
CYK算法,用于验证一个单词是否属于一个文法(Grammatik)。
4.8 Kellerautomaten
Pushdown Automaton (PDA)
4.9 Äquivalenz von PDAs und CFGs
4.10 Deterministische Kellerautomaten
4.11 Tabellarischer Überblick
5. Berechenbarkeit, Entscheidbarkeit
5.1 Der Begriff der Berechenbarkeit
Berechenbarkeit,Turingmaschine
5.2 Unentscheidbarkeit des Halteproblems
5.3 Semi-Entscheidbarkeit
5.4 Die Sätze von Rice und Shapiro
5.5 Das Postsche Korrespondenzproblem
5.6 Unentscheidbare CFG-Probleme
6. Komplexitätstheorie
- 6.1 Die Komplexitätsklasse P
- 6.2 Die Komplexitätsklasse NP
- 6.3 NP-Vollständigkeit
- 6.4 Weitere NP-vollständige Probleme
- 6.5 Die Unvollständigkeit der Arithmetik
- 6.6 Die Entscheidbarkeit der Presburger Arithmetik
需要掌握的算法:
第三章:
- Grammatik转NFA(Satz 3.9;H 3.1,T 2.2)
NFA转DFA (Satz 3.10)
- Potenzmengenkonstruktion(H 3.2)
DFA转Grammatik (Satz 3.13)
- epsilon-NFA转NFA(Lemma 3.16)
NFA转regulär Ausdruck
- 画图(T 4.1)
- 高斯消元/解方程/Ardens Lemma(T 4.2,H 4.1)
Regulär Ausdruck转epsilon-NFA(T 3.3,H 3.4)
- DFA Minimierung(Tabelle)(T 5.3 a),H 5.3)
- 构造regulär Ausdruck对应的Minimalautomat
第四章:
- 构造CFG的Chomsky-Normalform(T 7.1,T 7.4,H 7.1)
- 消除Grammatik的unnützliche Symbole(T 8.1,H 8.1)
- CYK(CYK Tabelle,用于验证一个单词是否属于一个文法(Grammatik))(T 8.2 b),T 8.5,H 8.2.)
- Grammatik转PDA(Satz 4.53,T 9.3)
- CFG转PDA
- PDA转CFG
不同Type的语言以及对应的自动机:
| Typ | Automat |
|---|---|
| Typ 3 | (Deterministischer) Endliche Autoamt / deterministic finite automaton (FA) |
| Typ 2 | Kellerautomat / Pushdown Automaton (PDA) |
| Typ 0 | Turingmaschinen (TM) |
基本概念
Definition:
一个
字母表(Alphabet)$\Sigma$ 是一个有限集合。
例如:$ \{0,1\} $、ASCII、Unicode。一个
单词/字符串 (Wort/String)是由$\Sigma$中字符组成的有限序列,例如 010。$|w|$表示单词$ w $ 的长度。
空单词(leere Wort)(长度为 0 的唯一单词)用$\varepsilon$表示。如果 $u$ 和 $v$ 是单词,则 $uv$ 表示它们的
连接(Konkatenation)。如果 $ w $ 是一个单词,那么 $w^n$ 定义为:
$ w^0 = \varepsilon $,并且 $ w^{n+1} = w w^n $。
例如:$ (ab)^3 = ababab $。$ \Sigma^* $ 是所有由 $ \Sigma $ 中字符组成的单词的集合(Menge aller Wörter)。
其中的子集$ L \subseteq \Sigma^* $ 被称为
(形式)语言 ((formale) Sprache)。
注意,这里的形式语言((formale) Sprache)$L$并没有要求必须包含$\varepsilon$。
来看一下简单的(形式)语言 ((formale) Sprache)的例子:
杜登(Duden)词典中所有单词的集合
$L_1 = \{ \varepsilon, ab, abab, ababab, \dots \} = \{ (ab)^n \mid n \in \mathbb{N} \}$
($\Sigma_1 = \{a, b\}$)
$L_2 = \{ \varepsilon, ab, aabb, abab, abba, baab, baba, bbaa, \dots \} = \{ w \in \{a,b\}^* \mid w\ \text{中包含相同数量的}\ a\ \text{和}\ b\ \text{字符} \}$
($\Sigma_2 = \{a, b\}$)
$L_3 = \{0, 1, 100, 1001, 10000, \dots\} = \{ w \in \{0,1\}^* \mid w\ \text{是一个二进制编码的平方数} \}$
($\Sigma_3 = \{0,1\}$)
$\emptyset$
$\{\varepsilon\}$
反例:
- $\varepsilon$ 或 $ab$ 不是语言,因为它们不是集合。
Definition: 语言上的运算(Operationen auf Sprachen)
设 $A, B \subseteq \Sigma^*$:
连接(Konkatenation):$AB := \{ uv \mid u \in A \land v \in B \}$
例子:$\{ab, b\} \{a, bb\} = \{aba, abbb, ba, bbb\}$例子:$\{ab, ba\}^2 = \{abab, abba, baab, baba\}$
递归定义:$
A^0 = \{\varepsilon\} \quad \text{且} \quad A^{n+1} := A A^n$
- 例子:
注意,因为$A^0 = \{ \varepsilon \}$,所以对于所有 $A$ 都有:$\varepsilon \in A^$,并且 $\emptyset^ = \{ \varepsilon \}$。
Lemma:
- $\emptyset A = \emptyset$
- $\{\varepsilon\}A = A$
证明:Trivial。$\square$
Lemma:
- $A(B \cup C) = AB \cup AC$
- $(A \cup B)C = AC \cup BC$
证明:Trivial。$\square$
但是注意,$A(B \cap C) \neq AB \cap AC$不一定一直成立。
反例:$A=\{a,ab\}, B=\{b\}, C =\{\varepsilon\}$:
最根本的原因是可能存在$u’v’= u’’v’’ \in AB \cap AC$并且$u’ \neq u’’, v’ \neq v’’$。这就导致不能从$uv \in AB \cap AC$推出存在$u \in A, v \in B \cap C$。
Lemma:
证明:Trivial。$\square$
文法(Grammatiken)
Definition:
一个文法(Grammatik)是一个四元组 $G = (V, \Sigma, P, S)$,其中:
$V$ 是一组
非终结符号(Nichtterminalzeichen / Nichtterminale / Variablen)的有限集合;$\Sigma$ 是一组
终结符号(Terminalzeichen / Terminale / Alphabet),与 $V$ 不相交;是一组
产生式(Produktionen)的集合;$S \in V$ 是
开始符号(Startsymbol)。
为了方便,我们一般用:
- $\alpha \to \beta$ 指代 $(\alpha, \beta) \in P$;
- $\alpha \to \beta_1|\cdots |\beta_n$ 指代 $\alpha \to \beta_1, …, \alpha \to \beta_n$
Definition:
一个文法(Grammatik) $G = (V, \Sigma, P, S)$ induziert 一个推导关系 $\to_G$,作用于 $V \cup \Sigma$ 上的单词:
当且仅当存在一条规则 $\beta \to \beta’$ 属于 $P$,以及单词 $\alpha_1, \alpha_2$,使得
一个这样的序列
叫做从 $\alpha_1$ 开始的推导(Ableitung)。
如果 $\alpha_1 = S$ 并且
,那么 $G$ 生成(erzeugt)单词 $\alpha_n$。
$G$ 的语言(Sprache von G)是所有由 $G$ 生成的单词的集合,记为 $L(G)$。
注意,定义里的$\alpha_1, \alpha_2$可以是$\varepsilon$,也可以是其他单词的Konkatenation。所以在一个大的Konkatenation里,对于其中一个存在Produktion,那么对整个Konkatenation都存在一个推导。
例子:
$V = \{ \langle \text{Expr} \rangle, \langle \text{Term} \rangle, \langle \text{Factor} \rangle \}$
$\Sigma = \{ a, b, c, +, *, (, ) \}$
$S = \langle \text{Expr} \rangle$
$P$:
该如何从$\langle \text{Expr} \rangle$推导出$a * (b + c)$呢?
一共需要11步。
例子:
这两个语法:
哪个可以生成$M = \{ a^n b^n c^n \mid n \geq 0 \}$呢?
首先,有$M \subseteq L(G_1)$,因为$S \to abcS \to abcabcS \to abcabc \to abacbc \to aabcbc \to aabbcc$。
只不过$L(G_1) \neq M$,因为$S \to abcS \to abcabcS \to abcabc$。
而$L(G_2) = M$,因为:
Definition: (Reflexive transitive Hülle)
不难注意到有:
例子:在前面的例子我们已经看到了$\langle \text{Expr} \rangle$推导出$a * (b + c)$需要11步,所以有
并因此有
和
乔姆斯基体系(Chomsky Hierarchie)
Definition:
一个文法 $G$ 的类型定义如下:
类型 0:始终成立。
类型 1:如果对于每一个产生式 $\alpha \to \beta$(除了 $S \to \varepsilon$)都有
并且,如果 $S \to \varepsilon$ 是一个产生式,则 $S$ 不出现在任何 $\beta$ 中。
类型 2:如果 $G$ 是类型 1 的文法,并且对于每个产生式 $\alpha \to \beta$,都有
类型 3:如果 $G$ 是类型 2 的文法,并且对于每个产生式 $\alpha \to \beta$(除了 $S \to \varepsilon$)都有
显然有:
Theorem:
| Typ | Grammatikart | Sprachklasse |
|---|---|---|
| Typ 3 | Rechtslineare Grammatik | Reguläre Sprachen |
| Typ 2 | Kontextfreie Grammatik | Kontextfreie Sprachen |
| Typ 1 | Kontextsensitive Grammatik | Kontextsensitive Sprachen |
| Typ 0 | Phrasenstrukturgrammatik | Rekursiv aufzählbare Sprachen |
Wortproblem:
Gegeben: 一个文法 $G$ 和一个单词 $w \in \Sigma^*$,
Frage:$w$ 是否属于 $L(G)$?
不同Type的语言以及对应的自动机:
| Typ | Automat |
|---|---|
| Typ 3 | (Deterministischer) Endliche Autoamt / deterministic finite automaton (FA) |
| Typ 2 | Kellerautomat / Pushdown Automaton (PDA) |
| Typ 0 | Turingmaschinen (TM) |
正规语言(Reguläre Sprachen)
等价关系:
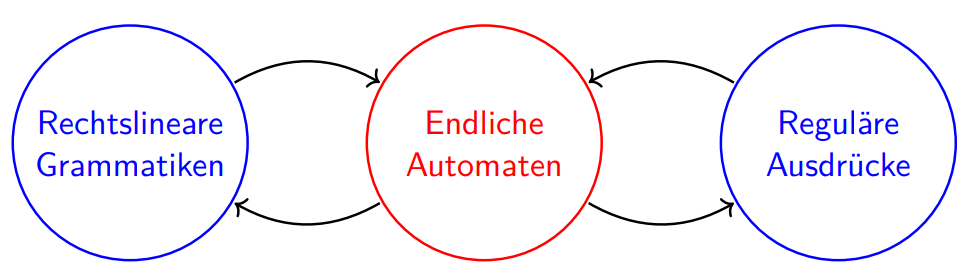
Deterministische endliche Automaten
Definition:
Ein deterministischer endlicher Automat (deterministic finite automaton, DFA)
$M = (Q, \Sigma, \delta, q_0, F)$ besteht aus
- einer endlichen Menge von Zuständen $Q$,
- einem (endlichen) Eingabealphabet $\Sigma$,
- einer (totalen!) Übergangsfunktion $\delta : Q \times \Sigma \rightarrow Q$,
- einem Startzustand $q_0 \in Q$, und
- einer Menge $F \subseteq Q$ von Endzuständen (akzeptierenden Zust.).
名字里的deterministisch是指:对于每一个状态(Zustand)以及一个Übergang只对应一个状态(Zustand)。
Definition:
Die von $M$ akzeptierte Sprache ist
wobei $\hat{\delta} : Q \times \Sigma^* \rightarrow Q$ induktiv definiert ist durch:
( $\hat{\delta}(q, w)$ bezeichnet den Zustand, den man aus $q$ mit $w$ erreicht. )
Eine Sprache ist regulär gdw. sie von einem DFA akzeptiert wird.
可以这样理解$\hat{\delta}$:第一个参数是起始状况(Zustand),然后第二个参数的一连串的路径(或者说是操作),会依次触发/经过。
所以
里的元素翻译一下就是:所有从起点到终点的路径/操作序列。
所有endliche Automaten都可以用gerichtete und makierte Zustandsgraph表示出来,其中
- 点(Knoten)代表Zustände;
- 线(Kanten)表示Übergänge $p \xrightarrow{a} q$ ,即$\delta(p,a)= q$;
- Anfangszustand 会被用一个箭头(Pfeil)标记出来;
- Endzustände 会被用doppelte Kreise标记出来。
例子:
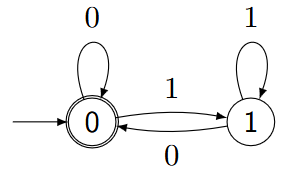
- $Q = \{0,1,2\}$
- $\Sigma = \{a,b\}$
不难注意到,在这里例子里,所有可以被akzeptiert的Wort都一定包含ab。(相当于必经之路)
同样,所有包含ab的Wort也一定会被akzeptiert。
例子:
我们用#w表示w的二进制。(比如说#100=4)

不难发现,DFA akzeptiert $w \in \{0,1\}^*$当且仅当#w是偶数。
证明:
假设$w \neq \varepsilon$,可以通过
可以得到
即$w \in L(A) \Leftrightarrow w\text{为偶数}$。(也就是二进制的最低位等于0)
如果$w = \varepsilon$,有$\hat{\delta}(0, \varepsilon) = 0$,所以$\varepsilon \in L(A)$。(注意 #$\varepsilon = 0$)$\square$
Von rechtslinearen Grammatiken zu DFA (und zurück)
Rechtslineare Grammatik(即Typ3)指的是所有Produktion都长这样:$A \to a$ 或者$A \to aB$。
Definition:
Ein nichtdeterministischer endlicher Automat (nondeterministic finite automaton, NFA) ist ein 5-Tupel
$N = (Q, \Sigma, \delta, q_0, F)$, so dass
- $Q$, $\Sigma$, $q_0$ und $F$ sind wie bei einem DFA
- $\delta : Q \times \Sigma \rightarrow \mathcal{P}(Q)$
- $\mathcal{P}(Q)$ = Menge aller Teilmengen von $Q$
- Alternative: Relation $\delta \subseteq Q \times \Sigma \times Q$
注意,在DFA里,每一个状态(Zustand)以及一个Übergang只对应一个状态(Zustand)。而在NFA里,一个状态(Zustand)以及一个Übergang可以对应多个状态。
例子:
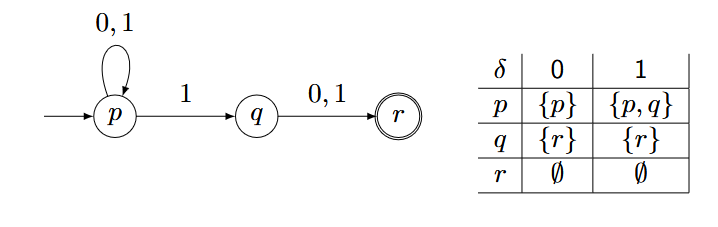
每一个点可能会拥有多条相同名字的边,所以结果是不确定的。(nichtdeterministisch )
当我们输入$0111$,可能会得到多个Zustandsfolgen:
和之前类似,我们可以在$\delta$的基础上定义
并在这个基础上像之前一样inductive定义
而$\hat{\delta}(S, w)$ 可以理解成是Menge aller Zustände, die sich von einem Zustand in $S$ aus mit $w$ erreichen lassen.
例子:

也就是说从$p,q$出发,进行一遍$10$的操作,最后一定会落在$p,r$。
Definition:
Die von $N = (Q, \Sigma, \delta, q_0, F)$ akzeptierte Sprache ist:
注意,在DFA定义的akzeptierte Sprache里,是
而在这里,由于$\hat{\delta}(q_0, w)$ 是几个集合,所以我们要求的是它和$F$的交集不为空,也就是说只要存在到达的可能性那就会被akzeptiert。
为了方便,我们后续一般还是用$\delta$ 指代$\bar{\delta}$ , $\hat{\delta}$ 指代$\hat{\bar{\delta}}$ 。
Theorem:
Für jede rechtslineare Grammatik $G$ gibt es einen NFA $N$ mit
主要的构造(证明)思路就是将Grammatik里的Variablen (V)构造成NFA的Zustände(Q),然后将Grammatik的Produktion构造成NFA里的Übergänge。
我们来看一下针对下面这个比较allgemein的例子的具体构造。
例子:
证明(构造):
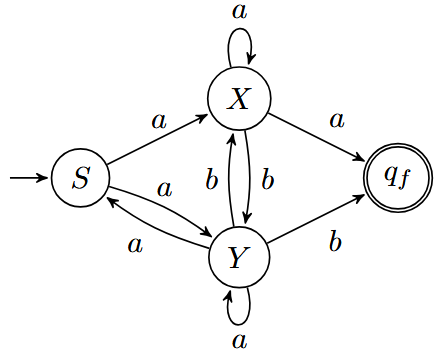
Sei $G = (V, \Sigma, P, S)$ eine rechtslineare Grammatik ohne die Produktion $S \rightarrow \varepsilon$.
Definiere den NFA $A = (Q, \Sigma, \delta, q_0, F)$ mit:
- $Q = V \cup \{q_f\}$ (wobei $q_f \notin V$)
- $Y \in \delta(X, a)$ gdw $(X \rightarrow aY) \in P$
- $q_f \in \delta(X, a)$ gdw $(X \rightarrow a) \in P$
- $q_0 = S$
- $F = \{q_f\}$
Es gilt: $a_1 \ldots a_n \in L(G)$
– gdw es existieren Variablen $X_1, \ldots, X_{n-1}$
– gdw es existieren Zustände $X_1, \ldots, X_{n-1}$
– gdw $a_1 \ldots a_n \in L(A)$
. $\square$
假设这个Grammatik还包含了$S \to \varepsilon$,那么需要将$F$构造成$F= \{S, q_f\}$。
Theorem:
Für jeden NFA $N$ gibt es einen DFA $M$ mit
证明:
Sei $N = (Q, \Sigma, \delta, q_0, F)$ ein NFA.
Definiere den DFA $M = (\mathcal{P}(Q), \Sigma, \bar{\delta}, \{q_0\}, F_M)$:
Dann gilt:
. $\square$
这种构造叫做 Potenzmengenkonstruktion 或者 Teilmengenkonstruktion。
注意,按照这个构造,如果NFA里有n个Zustände, 那对应的DFA里会有$2^n$个Zustände。很多当然是可以避免这个规格的,但是有些时候并避免不了。在这个Corollary之后我们会看一个避免不了的例子。
Corollary:
Für jede rechtslineare Grammatik $G$ gibt es einen DFA $M$ mit
例子:
(注意,这里是倒数第$k$位为1,不是正数。)
Ein NFA für diese Sprache:

Lemma:
Jeder DFA $M$ mit $L(M) = L_k$ hat mindestens $2^k$ Zuständen.
证明:
我们需要做的是证明 für alle $w_1, w_2 \in \{0, 1\}^k$:
证明了这个之后,由于$\{0, 1\}^k$里有$2^k$个元素,那么任意一个DFA里也至少会有$2^k$个Zusände,因为对于所有的$w \in \{0, 1\}^k$,$\hat{\delta}(q_0, w)$都是$M$里的一个Zustand。
那么我们现在开始证明这个结论,用反证法:
Annahme: Es gibt $w_1, w_2 \in \{0, 1\}^k$ mit $w_1 \ne w_2$, aber $\hat{\delta}(q_0, w_1) = \hat{\delta}(q_0, w_2)$.
Sei $w_1 = wa_i \ldots a_k$ und $w_2 = wb_i \ldots b_k$ mit $a_i \ne b_i$ ($i$表示的是$w_1,w_2$第一个不相等的位。而前面相同的部分我们就简单记作$w$。)
o.E. sei $a_i = 1$, $b_i = 0$.
Es gilt einerseits:
(在$w_1,w_2$后面加上$i-1$个0,这样一来第一个的倒数第$k$位就是1,第二个的倒数第$k$位是0。)
Aber es gilt auch:
但是根据$L(M)$的定义:
不可能存在$a,b$满足$\hat{\delta}(q_0, a) = \hat{\delta}(q_0, b)$,但是一个在$L(M)$,一个不在。
所以说得到一个Wiederspruch. $\square$
Theorem:
Für jeden DFA $M$ gibt es eine rechtslineare Grammatik $G$ mit
证明:
Sei $M = (Q, \Sigma, \delta, q_0, F)$.
Die Grammatik $G = (V, T, P, S)$ mit:
- $V = Q$, $T = \Sigma$, $S = q_0$
- $(q_1 \rightarrow aq_2) \in P$ gdw $\delta(q_1, a) = q_2$
- $(q_1 \rightarrow a) \in P$ gdw $\delta(q_1, a) \in F$
- $(q_0 \rightarrow \varepsilon) \in P$ gdw $q_0 \in F$
ist von Typ 3 und erfüllt $L(M) = L(G)$.$\square$
NFAs mit $\epsilon$-Übergängen
Definition:
Ein NFA mit $\epsilon$-Übergängen (auch $\varepsilon$-NFA) ist ein NFA mit einem speziellen Symbol $\epsilon \notin \Sigma$ und mit
Ein $\epsilon$-Übergang darf ausgeführt werden, ohne dass ein Eingabezeichen gelesen wird.
注意,这里的$\epsilon$和之前用的$\varepsilon$是不一样的东西。
$\epsilon$ ist ein einzelnes Symbol, $\varepsilon$ ist das leere Wort.
例子:
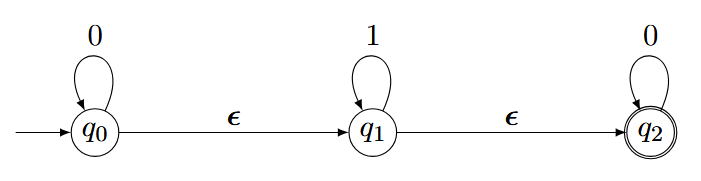
这个$\varepsilon$-NFA可以接受$\varepsilon,00,11,…$,但不能接受$101,…$。
也就是说,这个Automat虽然读取的是$11$,但它可以先(“免费”)跳到$q_1$,然后再进行2次$1$的操作。
Lemma:
Für jeden $\epsilon$-NFA $N$ gibt es einen NFA $N’$ mit
证明:
Sei $N = (Q, \Sigma, \delta, q_0, F)$ ein $\epsilon$-NFA.
Wir definieren den NFA
$N’ = (Q, \Sigma, \delta’, q_0, F’)$ mit folgenden Definitionen für $\delta’$ und $F’$:
$\delta’ : Q \times \Sigma \rightarrow \mathcal{P}(Q)$
Falls $N$ das leere Wort $\varepsilon$ akzeptiert, also falls
dann setze $F’ := F \cup \{q_0\}$, sonst setze $F’ := F$.$\square$
例子:
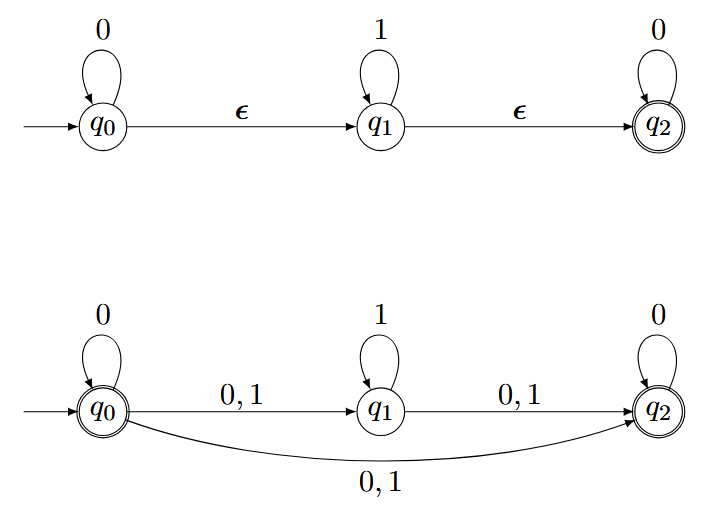
Reguläre Ausdrücke 正则表达式
Berechenbarkeit, Entscheidbarkeit
Begriffe
图灵机 (Turing Maschine)
可以这样理解:机器会(依靠一个探头 read/write head)读取一条Band上的内容,然后根据当前位置进行以下操作:
- 调整当前位置
- 改写Band当前位置的值
- 调整探头位置(左/右/不动)




